SIMULASI DAN LATIHAN SOAL

TINKERCAD 

tampilan dashboard tinkercad ketika sudah terdaftar

    Tinkercad merupakan sebuah platform yang merupakan web penyedia sarana bagi kita untuk belajar secara online terkait desain 3d, rangkaian elektronika dan codeblock. Tinkercad merupakan web besutan dari Autodesk yang sudah cukup terkenal. Jika sebelum-sebelumnya Autodesk banyak memperkenalkan software-software komputer seperti software desain, animasi, kini mereka hadir dengan salah satu platform yang bernama Tinkercad. Sebenarnya, web ini sudah lama didirikan yakni pada tahun 2011. Walaupun begitu, pengembangan web ini masih berlanjut dan menjadi salah satu web yang saya rekomendasikan untuk digunakan sebagai media pembelajaran.

Pengertian IC (Integrated Circuit)

    IC (Integrated Circuit) adalah komponen elektronika semi konduktor yang merupakan gabungan dari ratusan atau ribuan komponen-­komponen lain. Bentuk IC berupa kepingan silikon padat, biasanya berwarna hitam yang mempunyai banyak kaki-­kaki (pin) sehingga bentuknya mirip sisir. IC merupakan gabungan dari beberapa komponen seperti Resistor, Kapasitor, Dioda dan Transistor yang telah terintegrasi menjadi sebuah rangkaian berbentuk chip kecil, 

    IC digunakan untuk beberapa keperluan pembuatan peralatan elektronik agar mudah dirangkai menjadi peralatan yang berukuran relatif kecil. Sebelum adanya IC, hampir seluruh peralatan elektronik dibuat dari satuan­-satuan komponen (individual) yang dihubungkan satu sama lainnya menggunakan kawat atau kabel, sehingga tampak mempunyai ukuran besar serta tidak praktis. 

Sejarah IC (Integrated Circuit)

    IC (Integrated Circuit) adalah nama lain chip. IC adalah piranti elektronis yang dibuat dari material semikonduktor. IC atau chip merupakan cikal bakal dari  sebuah komputer dan segala jenis device yang memakai teknologi micro­controller lainnya. IC ditemukan pada tahun 1958 oleh seorang insinyur bernama Jack Kilby yang bekerja pada Texas Intruments mencoba memecahkan masalah dengan memikirkan sebuah konsep menggabungkan seluruh komponen elektronika dalam satu blok yang dibuat dari bahan semikonduktor. 

   Penemuan itu kemudian dinamakan IC (Integrated Circuit) atau yang kemudian lazim disebut chip. Beberapa saat setelah itu, Robert Noyce, yang bekerja pada Fairchild Semiconductor Corporation, menemukan hal serupa, meskipun mereka bekerja pada dua tempat yang berbeda. Semenjak itu banyak riset yang dilakukan untuk mengembangkan IC (Integrated Circuit) atau Chip hingga saat ini. 

   Seorang pendiri Intel, Gorden Moore, pada tahun 1965 memperkirakan bahwa jumlah transistor yang terdapat dalam sebuah IC akan bertambah 2 kali setiap 18 bulan sekali. Kecenderungan peningkatan jumlah transistor ini telah terbukti setelah sekian lama dan diperkirakan akan terus berlanjut. Hal ini dapat dilihat pada perkembangan IC, sebuah 64­Mbit DRAM yang pertama kali di pasaran pada tahun 1994, terdiri dari 3 juta transistor. Dan microprocessor Intel Pentium 4 terdiri lebih dari 42 juta transistor dan kira­kira terdapat 281 IC didalamnya. 

  Bahkan berdasar pada International Technology Roadmap for Semiconductor (ITRS), diharapkan akan tersedia sebuah chip yang terdiri dari 3 milyar transistor pada tahun 2008.

     IC sendiri dipergunakan untuk bermacam-­macam piranti, termasuk televisi, telepon seluler, komputer, mesin-­mesin industri, serta berbagai perlengkapan audio dan video. IC sering dikelompokkan berdasar jumlah transistor yang dikandungnya: 

• SSI (Small­Scale Integration) : chip dengan maksimum 100 komponen elektronik.  

• MSI (Medium­Scale Integration):chip dengan 100 sampai 3.000 komponen elektronik 

• LSI (Large­Scale Integration) : chip dengan 3.000 sampai 100.000 komponen elektronik. 

• VLSI (Very Large­Scale Integration): chip dengan 100.000 sampai 1.000.000 komponen elektronik. 

• ULSI (Ultra Large­Scale Integration) : chip dengan lebih dari 1 juta komponen elektronik. 

1.     IC GERBANG LOGIKA AND

Ada banyak sekali contoh IC gerbang logika AND dengan beragam spesifikasi teknis, mulai dari IC TTL hingga IC CMOS. Berikut beberapa diantaranya tipe IC yang berisi gerbang AND:

IC 7408 berisi empat gerbang AND dengan dua input dari keluarga Transistor Transistor Logic

IC 7411 berisi tiga gerbang AND dengan tiga input dari keluarga Transistor Transistor Logic

IC 4081 berisi empat gerbang AND dengan dua input dari keluarga CMOS

IC 4073 berisi tiga gerbang AND dengan tiga input dari keluarga CMOS

2.     IC GERBANG LOGIKA OR

Gerbang-gerbang logika dapat ditemui dipasaran dalam bentuk chip atau IC. berikut ini adalah IC untuk gerbang logika OR.

1. C dari keluarga TTL : 74LS32 quad 2 input OR GATE
2. IC dari keluarga CMOS : CD4071 quad 2 input OR GATE
3. IC dari keluarga CMOS : CD4075 Tripe 3 input OR GATE
4. IC dari keluarga CMOS : CD4072 Dual 4 input OR GATE

Gambar konfigurasi kaki IC – iC tersebut dapat dilihat pada gambar berikut:

3.      IC GERBANG LOGIKA NOT

-    Gerbang NOT

Sebuah inverter logika, kadang disebut gerbang NOT untuk membedakannya dari jenis - jenis perangkat inverter elektronik lainnya, gerbang NOT hanya memiliki satu masukan. Gerbang NOT membalikkan keadaan logika. Penggunaan gerbang NOT yang paling terkenal yaitu pada IC 7404. IC ini mempunyai enam gerbang NOT didalamnya. Untuk membuatnya bekerja kita perlu menghubungkannya dengan power supply 5 volt.

 Inverter or NOT gate

Input	Output
1
	1

IC 7404

GERBANG LOGIKA – GATE OR IC TTL 7432

Gerbang Logika atau dalam bahasa Inggris disebut dengan Logic Gate adalah dasar pembentuk Sistem Elektronika Digital yang berfungsi untuk mengubah satu atau beberapa Input (masukan) menjadi sebuah sinyal Output (Keluaran) Logis. Gerbang Logika beroperasi berdasarkan sistem bilangan biner yaitu bilangan yang hanya memiliki 2 kode simbol yakni 0 dan 1 dengan menggunakan Teori Aljabar Boolean.

IC TTL 7432

IC TTL adalah IC yang banyak digunakan dalam rangkaian digital karena menggunakan sumber tegangan (VS) antara 4,75 Volt sampai 5,25 Volt. Komponen pembangun IC TTL(transistor-transistor logic) adalah sesuai dengan namanya IC ini berisi beberapa transistor yang digabungkan sehingga membentuk dua keadaan (ON/FF).

Gerbang ini sudah terkemas dalam IC tipe 7432. Sama dengan gerbang AND, gerbang OR hanya memiliki 2 buah input dan 1 output, sehingga dibutuhkan 2 gerbang untuk menjadikan 3 input dan 1 output.

Pada output akan berharga 1 (indicator menyala) jika salah satu atau semua dari inputnya diberi masukan sebesar Vcc. Sebaliknya jika semua input diberi masukan dari ground atau terlepas, maka output akan berharga 0 (indicator tidak menyala).

Jika Anda ingin mencoba membuat rangkaian ini, harga  IC TTL 7432 yang berada di pasaran adalah +/- Rp. 3.300 perak, murah bukan ? 

Gerbang Logika dan Aljabar boolean part 3

     Memahami Peta Karnaugh

Peta Karnaugh adalah sebuah metode untuk:

1. Menyederhanakan sebuah fungsi persamaan logika. Menyederhanakan fungsi persamaan logika sebenarnya bisa dilakukan dengan menggunakan aturan-aturan baku seperti:

• Distributif. Misalnya (p ∧ q) ∨ (p ∧ r) ≡ p ∧ (q ∨ r)  atau (p ∨ q) ∧ (p ∨ r) ≡ p ∨ (q ∧ r). 
• De Morgan seperti ~p ∨ ~q ≡ ~(p ∧ q) atau ~p ∧ ~q
• Hukum penyerapan  seperti p ∧ (p ∨ q) ≡ p atau p ∨ (p ∧ q) ≡ p

2. Mencari fungsi persamaan logika dari sebuah tabel kebenaran. Terkadang, kita memiliki sebuah tabel kebenaran (yang diperoleh dari pengumpulan kasus atau kejadian) tetapi belum memiliki persamaan logikanya sehingga sulit membuat untai rangkaian logikanya.

Permasalahan-permasalahan diatas dapat diselesaikan dengan peta karnaugh.

Peta Karnaugh

Peta karnaugh (atau K-Map) diperkenalkan oleh Maurice Karnaugh tahun 1953 (wikipedia) adalah sebuah metode untuk menyederhanakan fungsi persamaan logika sehingga (Freddy Kurniawan: Sistem Digital):

1. Menggunakan jumlah gerbang lebih sedikit sehingga waktu tunda total untai menjadi lebih kecil
2. Kemungkinan resiko kegagalan fungsi lebih kecil karena penggunaan gerbang dan perkawatan yang lebih sedikit
3. Daya total yang dikonsumsi untai logika juga akan lebih kecil.
4. Hemat biaya

Peta Karnaugh di-"ilustrasikan" seperti matrik 2 dimensi (terdiri atas baris dan kolom) dimana komponen baris dan kolom adalah masukan (input) dari sistem. Input dari masukan inilah yang kemudian disebut variabel K-Map nya. Sehingga ada sebutan K-Map 2 Peubah, K-Map 3 Peubah, 4 peubah dst.

K-Map efektif digunakan hanya sampai 6 peubah saja. Untuk peubah lebih dari 6, tidak lagi di-rekomendasikan menggunakan K-Map karena komputasinya sangat tinggi sehingga disarankan menggunakan program komputer khusus. Tutorial kali ini, saya akan membahas K-Map hingga 4 Variabel. Untuk K-Map 5 dan 6 Peubah akan dibahas pada tutorial berikutnya.

Menggambar peta karnagh

Peta Karnaugh 2 Peubah:

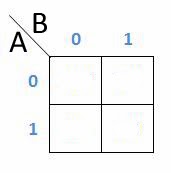
Ilustrasi berikut adalah peta karnaugh 2 peubah (A dan B).

Kelompok Baris adalah masukan A dan Kelompok Kolom adalah masukan B. Tidak ada yang spesial dari aturan K-Map 2 Variabel. Anda bisa menulisnya 0 kemudian 1 (sesuai contoh) atau 1 kemudian 0.

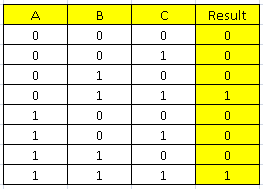
Sekarang kita lihat tabel kebenaran dari fungsi yang akan kita buat. Asumsikan, kita tidak memiliki fungsi persamaan dari tabel kebenaran berikut dan kita akan membuatnya.

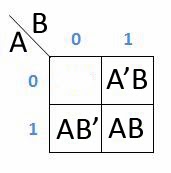
Setiap cell dari matrik (bagian tengah) akan kita isi dengan hasil atau result dari tabel kebenaran. Sebagai contoh:

Peta Karnaugh 3 Peubah:

Sedikit berbeda dengan peta karnaugh 2 peubah, K-Map 3 peubah menggunakan 2 peubah di satu rusuk dan 1 peubah di rusuk yang lain. Anda bisa membuat K-Map dengan 2 peubah di rusuk tegak, dan 1 peubah di rusuk mendatar atau sebaliknya. Perhatikan gambar:

Yang perlu diperhatikan di sini adalah penyusunan kombinasi masukan 2 peubah harus mengikuti kaidah "perubahan di satu tempat". Artinya transisi dari "0" ke "1" hanya di satu tempat saja. Sebagai contoh, kombinasi masukan dari "01" menjadi "11". Transisi yang terjadi pada kombinasi ini hanya pada masukan A (dari 0 menjadi 1) sedangkan masukan B tetap (1 tetap 1). Jadi anda tidak boleh menulis "01" kemudian "10" (seperti yang biasa anda lakukan di tabel kebenaran). Mengapa? karena jika susunan-nya "01" kemudian "10", berarti perubahan terjadi di 2 masukan, A berubah dari "0" menjadi "1" dan masukan B berubah dari "1" menjadi "0".

Seperti pada K-Map 2 peubah, isi Cell dari K-Map 3 peubah juga berisi result (hasil) dari tabel kebenaran. Sebagai contoh:

Anda boleh menggunakan K-Map yang atas atau yang bawah.

Peta Karnaugh 4 Peubah:

Untuk K-Map 4 peubah, anda dapat memasukkan 2 peubah di rusuk tegak dan 2 peubah di rusuk mendatar. Perhatikan gambar:

Daerah Minterm

Nah sekarang kita sudah bisa menggambar peta Karnaugh atau K-Map dengan 2, 3 dan 4 peubah. Proses berikutnya adalah menentukan daerah minterm. Daerah minterm adalah sebuah daerah di dalam K-Map yang berisi nilai 1 yang "bertetangga" (akan dijelaskan dalam contoh). Keanggotaan sebuah daerah minterm bisa berisi 2^n dimana n bernilai 0, 1, 2, 3, ... dst. Sehingga keanggotaan wilayah minterm bisa 1, 2, 4, 8, 16, dst.

Melukiskan daerah minterm, bisa secara vertikal (atas bawah) atau horisontal (kiri dan kanan) tetapi tidak bisa secara diagonal.

Contoh daerah minterm untuk K-Map 2 peubah adalah sebagai berikut:

Keterangan:

(A): Karena nilai "1" hanya ada satu, maka daerah mintermnya juga hanya 1.

(B): Nilai "1" ada di dua tempat (cell) tetapi mereka bertetangga secara diagonal, maka angka-angka "1" tersebut tidak bisa menjadi satu wilayah minterm.

(C): Terdapat 2 wilayah minterm dengan masing-masing memiliki 2 anggota angka "1".

(D): Mirip dengan kasus point (B).

Sedikit berbeda untuk K-Map dengan dimensi yang lebih besar(di atas dimensi 2x2), K-Map "dipandang sebagai sebuah bidang yang "bulat" seperti globe. Artinya daerah minterm bisa saja "menyatukan" angka 1 yang di sisi atas dan bawah atau kiri dan kanan secara berputar. Lihat contoh di bawah ini:

Ingat: Tidak bisa diagonal saja.

Membangun persamaan dari daerah minterm di K-Map

Setelah daerah minterm sudah kita tandai, proses berikutnya adalah menentukan persamaan dari daerah minterm tersebut. Kita bisa menggunakan asas "konsistensi" untuk memudahkan membangun persamaan daerah minterm tersebut. Konsistensi yang saya maksud adalah nilai masukan yang TIDAK BERUBAH di setiap sel daerah minterm. Sebagai contoh untuk daerah minterm yang hanya berisi satu anggota seperti pada gambar berikut:

Karena kita tidak bisa membuat daerah minterm secara diagonal maka K-Map di atas memiliki 2 daerah minterm. Untuk daerah mintem yang berisi satu anggota saja, membuat persamaannya cukup mudah. Cukup lihat masukan untuk setiap daerah minterm tersebut.

Daerah minterm 1: masukan dari sisi baris adalah A'B dan dari sisi kolom adalah C'. Nilai akses (') di sini mengacu pada nilai 0 pada masukan A dan C (sedangkan karena nilai B bernilai "1" maka tidak diberi aksen atau NOT).

Daerah minterm 2: masukan dari sisi baris adalah AB dan dari sisi kolom adalah C (semua nilai masukan "1" maka tidak ada aksen)

Sehingga fungsi persamaan dari K-Map tersebut adalah: A'BC + ABC.

Pembuktian dengan tabel kebenaran:

Untuk daerah minterm yang berisi lebih dari satu, asas konsistensi bisa kita gunakan. Perhatikan contoh:

Pada contoh di atas, daerah mintem yang terbentuk memiliki empat anggota dimana masukannya adalah:

1. Sisi Baris (AB): 01 dan 11
2. Sisi Kolom (CD): 01 dan 11

Nilai yang konsisten di sisi baris adalah B. (A tidak konsisten karena ada A yang bernilai "1" dan ada A yang bernilai "0". Sedangkan nilai yang konsisten di sisi kolom adalah D. (nilai C tidak konsisten).

Sehingga persamaan untuk K-Map di atas adalah BD. Lihat pada tabel kebenaran berikut:

Contoh lain:

Daerah minterm 1 (yang berwarna biru): Masukan yang konsisten di sisi baris (masukan AB) adalah B dan masukan yang konsisten di sisi kolom adalah C sehingga rumus fungsinya adalah BC

Daerah minterm 2 (yang berwarna merah): Masukan yang konsisten di sisi baris (masukan AB) tidak ada (semuanya (baik A dan B) tidak ada yang konsisten) sedangkan masukan yang konsisten di sisi kolom adalah CD'.

Sehingga persamaan fungsi dari K-Map di atas adalah F = BC + CD'. Perhatikan tabel kebenaran berikut:

     langkah-langkah penyelesaian dengan metode karnaugh map

1. Menyusun aljabar Boolean terlebih dahulu

2. Menggambar rangkaian digital

3. Membuat Table Kebenarannya

4, Merumuskan Tabel Kebenarannya

5. memasukkan rumus Tabel Kebenaran ke K-Map (Kotak-kotak)

Gambar 1. Penyederhanaan menggunakan K-Maps

    contoh penyelesaian soal dengan karnaugh map variabel

Penyederhanaan Dua Variabel

Catatan : Bar = ‘

Tabel dari K-Map 2 variabel adalah seperti dibawah ini

Contoh Soal :

H = AB + A’B+AB’

Maka cara pengerjaanya seperti dibawah ini

Bar (‘) atau aksen biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar aksen.

Dan dapat dipermudah lagi menjadi dibawah ini :

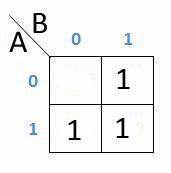
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya:

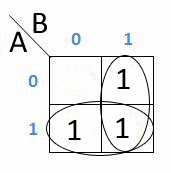
Karena kolom ber angka 1 dan baris ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau H = AB + A’B+AB’ K-Map nya adalah AB/BA

Penyederhanaan Tiga Variabel

Catatan : Bar = ‘

Tabel dari K-Map 3 variabel adalah seperti dibawah ini

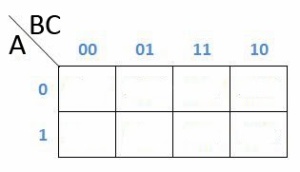
Contoh Soal

H = ABC + A’BC+A’B’C+AB’C

Maka cara pengerjaanya seperti dibawah ini

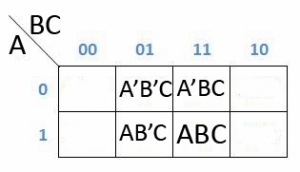
Dan dapat dipermudah lagi menjadi dibawah ini

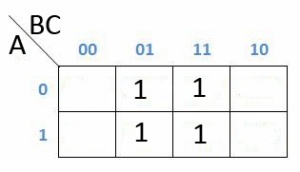
Sekarang kita lihat, karena yang memenuhi setiap kotaknya adalah baris 01 dan 11 sedangkan simbol 01 artinya adalah (B’C) dan 11 artinya adalah (BC) dan simbol yang tidak ada aksen nya hanya C, maka H = ABC + A’BC+A’B’C+AB’C adalah C.

Penyederhanaan empat variabel

Catatan : Bar = ‘

Tabel dari K-Map 4 variabel adalah seperti dibawah ini :

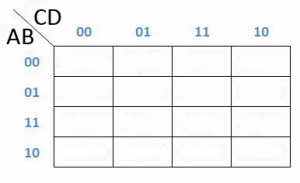
Contoh Soal

H = ABCD + ABCD’+AB’CD+ABC’D’

Maka cara pengerjaanya seperti dibawah ini

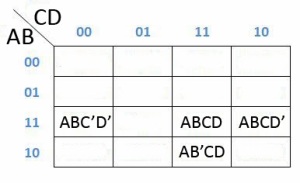
Dan dapat dipermudah lagi menjadi dibawah ini :

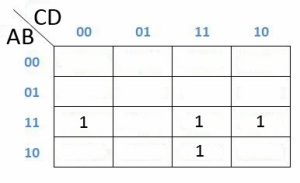
Karena yang ada angka 1 nya ada di kolom dan baris 1100, 1111, 1110 dan 1011, yaitu AB, ABCD, ABC dan ACD maka jika kita eliminasi dengan cara mengambil huruf yang sama saja menjadi AB + ABC + ACD.

Penyederhanaan 5 variabel

Gerbang logika dan aljabar boolean part 2

 GERBANG LOGIKA DAN ALJABAR BOOLEAN

1. Peran Gerbang Logika   

Gerbang logika dapat digunakan untuk merancang dan mendesain sistem digital yang dikendalikan oleh level masukan digital dan menghasilkan sebuah keluaran yang bergantung pada rangkaian logika itu sendiri. Gerbang logika banyak digunakan untuk praktek di laboratorium pada pembahasan mengenai elektronika digital.

2. Peran Aljabar Boolean

Aljabar Boolean atau dalam bahasa Inggris disebut dengan Boolean Algebra adalah matematika yang digunakan untuk menganalisis dan menyederhanakan Gerbang Logika pada Rangkaian-rangkaian Digital Elektronika. Boolean pada dasarnya merupakan Tipe data yang hanya terdiri dari dua nilai yaitu “True” dan “False” atau “Tinggi” dan “Rendah” yang biasanya dilambangkan dengan angka “1” dan “0” pada Gerbang Logika ataupun bahasa pemrograman komputer. Aljabar Boolean ini pertama kali diperkenalkan oleh seorang Matematikawan yang berasal dari Inggris pada tahun 1854. Nama Boolean sendiri diambil dari nama penemunya yaitu George Boole.

Penyederhanaan Logika

Metode Penyederhanaan Logika

Ada beberapa metode untuk menyederhanakan logika di antaranya :

a. Karnaugh Map

b. Diagram Venn

c. Quinne_Mc Cluskey

A.  Karnuagh Map

Karnaugh Map Method (metode peta Karnaugh ) adalah metode untuk menyederhanakan persamaan aljabar Boolean. Metode ini pertama kali diperkenalkan oleh Maurice Karnaugh pada tahun 1953 yang merupakan penyederhanaan dari metode Veitch Chart (Kartu Veitch).

Langkah-langkah menggunakan metode peta Karnaugh adalah sebagai berikut

1. Pastikan terlebih dahulu persamaan Boolen berada dalam bentuk standar. Dalam hal ini saya menggunakan standar SOP (Sum Of Product).

Contoh :

2. Susun tabel kebenaran untuk persamaan di atas

3. Buat peta Karnaugh dengan jumlah kotak 2n dengan n = banyaknya variabel. Dari contoh di atas, terdapat 3 variabel sehingga kotak peta Karnaugh adalah 23 = 8 kotak. Dan masukkan minterm (m) dari tabel kebenaran ke dalam kotak yang sesuai.

4. Buat loop atau kelompok pada minterm-minterm yang berdekatan dengan banyaknya anggota kelompok 1, 2, 4, 8 atau 16 supaya dapat dihilangkan minterm yang berlawanan.

Pada tabel Karnaugh di atas terdapat kelompok dengan 2 anggotam minterm yaitu kelompok biru dan kelompok merah. Masing-masing kelompok beranggotakan 2 minterm. Maka persamaan minimum dapat diperoleh dari gabungan minterm yang ada pada tiap-tiap kelompok yaitu :

5. Tulis ulang bentuk minimum dari persamaan aljabar Boolean yaitu :

6. Buat rangkaian digital dengan menggunakan persamaan minumum pada no 5

Gambar 1 rangkaian digital untuk persamaan no 5

Metoda peta Karnaugh sangat berguna dan efektif untuk mendesain rangkaian digital terutama untuk rangkaian-rangkaian digital dengan banyak variabel.

B. Diagram Venn

Salah satu cara untuk memudahkan untuk melukiskan hubungan antara variabel dalam aljabar boolean adalah dengan  menggunakan diagram venn. Diagram ini terdiri dari sebuah segi empat yang didalamnya dilukis lingkaran-lingkaran yang mewakili variabelnya, satu lingkaran untuk setiap variabelnya. Masing-masing lingkaran itu diberi nama menurut variabel yang diwakilinya. Ditentukan bahwa semua titik diluar lingkaran itu tidak dimiliki oleh variabel tersebut. Misalnya lingkaran dengan nama A, jika dalam lingkaran itu dikatakan bernilai 1, maka diluar a dikatakan bernilai 0. untuk dua lingkaran yang bertumpang tindih, terdapat empat daerah dalam segiempat tersebut.Diagram venn hanya cocok apabila jumlah variabelnya tidak lebih dari 3, karena bila lebih dari 3 variabel akan sulit menghitungnya.

3.2.1. Diagram Venn 2 Variabel.

c. MetodeQuinne_Mc Cluskey

Dengan Peta Karnaugh, penyelesaian persamaan lebih dari empat variabel adalah kompleks. Metode tabulasi dari Quine-Mc.Cluskey dapat membantuk menyelesaiakan persamaan 

yang kompleks tersebut.

Metode tabulasi Quine-Mc.Cluskey terdiri dari dua bagian, yaitu :

a.    Menentukan term-term sebagai kandidat (prime implicant)

b.    Memilih prime implicant untuk menentukan ekspresi dengan jumlah literal sedikit.

Contoh kasus :

Sederhanakan F(w,x,y,z) = ∑m(0,2,3,6,7,8,9,10,13)

Langkah – langkahnya adalah sebagai berikut :

A.    Menentukan term-term sebagai kandidat (prime implicant)

A.1.Susun tabel minterm,  bentuk biner dari minterm,  dan banyaknya angka 1 pada kode biner tersebut.

Minterm	Bentuk biner	Jumlah angka 1
m0	0000	0
m2	0010	1
m3	0011	2
m6	0110	2
m7	0111	3
m8	1000	1
m9	1001	2
m10	1010	2
m13	1101	3

Kelompok	Jumlah angka 1	Minterm	Bentuk biner
0	0	m0	0000
1	1 1	m2 m8	0010 1000
2	2	m3	0011
	2 2 2	m6 m9 m10	0110 1001 1010
3	3 3	m7 m13	0111 1101

A.2.Urutkan dan kelompokkan data pada tabel diatas berdasarkan jumlah angka 1 yang terdapat pada  kode binernya.

A.3Pasangkan dua buah minterm dengan ketentuan sebagai berikut :

-  Kedua minterm tersebut hanya memiliki perbedaan 1 digit pada kode binernya

-  Kedua minterm harus dari 2 kelompok yang berbeda dan dari kelompok yang berurutan

-  Mengganti digit yang berbeda dengan tanda “-” dan hasil pasangan yang didapatkan kita

masukkan ke tabel baru yang disebut tabel “Kubus-1”

Contoh 1 :

m0 (0000) dan m2 (0010) BOLEH dipasangkan.

Karena :

·   memiliki perbedaan 1 digit pada kode binernya yaitu digit 2-an

·   m0 dan m2 berasal dari dua kelompok yang berurutan yaitu kelompok-0 dan

kelompok-1

·   sebagai hasil pemasangannya adalah 00-0 (pada digit yang berbeda diganti dengan -)

·   setiap kali kita menyusun pasangan, jangan lupa untuk memberikan  tanda ( √ ) pada minterm yang terlibat, tanda ini sebagai pengingat bahwa minterm tersebut pernah  dipasangkan.

Secara keseluruhan pasangan yang BOLEH dilakukan antara lain :

Pasangan minterm	Hasil pasangan
m0 (kelompok 0) m2 (kelompok 1)	0000 0010 00 -0
m0 (kelompok 0) m8 (kelompok 1)	0000 1000 -000
m2 (kelompok 1) m3 (kelompok 2)	0010 0011 001-
m2 (kelompok 1) m6 (kelompok 2)	0010 0110 0-10
m2 (kelompok 1) m10 (kelompok 2)	0010 1010 -010
m8 (kelompok 1) m9 (kelompok 2)	1000 1001 100-
m8 (kelompok 1) m10 (kelompok 2)	1000 1010 10-0
m3 (kelompok 2) m7 (kelompok 3)	0011 0111 0-11
m6 (kelompok 2) m7 (kelompok 3)	0110 0111 011-
m9 (kelompok 2) m13 (kelompok 3)	1001 1101 1-01

Kelompok	Jumlah angka 1	Minterm	Bentuk biner	tanda
0	0	m0	0000	√
1	1 1	m2 m8	0010 1000	√ √
2	2	m3	0011	√
	2 2 2	m6 m9 m10	0110 1001 1010	√ √ √
3	3 3	m7 m13	0111 1101	√ √

Catatan :

O Tidak boleh  memasangkan  2  buah  minterm  yang  memiliki  perbedaan  lebih  dari  1  digit Pada kode binernya.

O Tidak  boleh  mernasangkan  2  buah  minterm  yang berasal  dari  dua  kelompok  yang tidak berurutan

Dari pemasangan yang dilakukan akan didapatkan table minterm dan table kubus-1 sebagai berikut :

Tabel Kubus-1
m0,m2 m0,m8	00-0 -000
m2,m3 m2,m6 m2,m10 m8,m9 m8,m10	001- 0-10 -010 100- 10-0
m3,m7 m6,m7	0-11 011-
m9,m13	1-01

Lakukan pemasangan serupa terhadap data hasli yang tertera pada kubus-1 dan tuliskan hasilnya pada kubus 2.

Kubus-1
m0,m2 m0,m8	00-0 -000	√ √
m2,m3 m2,m6 m2,m10 m8,m9 m8,m10	001- 0-10 -010 100- 10-0	√ √ √ ** √
m3,m7 m6,m7 m9,m13	0-11 011- 1-01	√ √ **

Catatan :

Tanda bintang ( ** ) menandakan bahwa minterm tersebut belum pernah mendapat pasangan pada proses membentukan tabel kubus berikutnya.

Minterm ini dinamakan sebagai Prime Implicant.

 

Kubus-2
m0,m2  &  m8,m10	-0-0
m0,m8  &  m2,m10	-0-0
m2,m3  &  m6,m7	0-1-
m2,m6  &  m3,m7	0-1-

Kubus-2
m0,m2  &  m8,m10	-0-0
m2,m3  &  m6,m7	0-1-

Jika pasangan minterm menghasilkan kode biner yang sama maka cukup ditulis salah satu saja. Sehingga tabel kubus-2 menjadi :

A.4.    Jika masih menungkinkan lakukan pemasangan lagi terhadap data pada kubus-kubus berikutnya hingga tidak ada lagi data pada kubus terakhir yang bisa dipasangkan lebih lanjut.

A.5.    Jika sudah tidak ada lagi yang bisa dipasangkan seperti pada kubus-2, sebenarnya kita sudah mendapatkan prime implikant.

Kubus-2
m0,m2  &  m8,m10	-0-0	**
m2,m3  &  m6,m7	0-1-	**

Pada contoh ini kita mendapatkan 4 prime implicant yaitu :

m8,m9                               →       1 0 0  -

m9,m13                             →       1 -  0 1

m0,m2 & m8,m10             →       -  0 -  0

m2,m3 & m6,m7                →         0 -  1 -

B.    Memilih prime implicant untuk menentukan ekspresi dengan jumlah literal sedikit

B.1  Susun tabel prime implicant (lihat tabel berikut ini).

Flag	Prime Implicant	m0	m2	m3	m6	m7	m8	m9	m10	m13
	m0,m2 & m8,m10	*	*				*		*
	m2,m3 & m6,m7		*	*	*	*
	m8,m9						*	*
	m9,m13							*		*

B.2  Beri tanda ‘√‘ pada kolom flag untuk kelompok prime implicant yang memiliki kolom bertanda * satu buah saja

Flag	Prime Implicant	m0	m2	m3	m6	m7	m8	m9	m10	m13
√	m0,m2 & m8,m10	ê	*				*		ê
√	m2,m3 & m6,m7		*	ê	ê	ê
	m8,m9						*	*
√	m9,m13							*		ê

Catatan :   pada  kelompok  prime  implicant  m8,  m9  tidak  diberi  tanda  ‘ê’  karena  tidak  memiliki kolom  yang  hanya  memua t satu  tanda  ‘* ’

B.3  Prime Implicant  yang  memiliki  tanda ‘ê ‘  adalah  yang  terpilih  untuk  penyusunan  fungsi boolean  yang  dimaksud.

 Susun fungsi boolean berdasarkan prime implicat yang terpilih, yaitu :

m0,m2 & m8,m10           :  - 0 – 0      →  x’ z’

m2,m3 & m6,m7             :  0 – 1 -     →  w’y

m9,m13                          :  1 – 0 1    →  wy’z

Jadi fungsi boolean yang dimaksud adalah :

F(w,x,y,z) = x’ z’ + w’y + wy’z

Bentuk Kanonik Dalam Aljabar Boolean

Contoh dan  POS  dan   SOP          

 Membuat ekspresi Boolean dalam bentuk SOP dan POS dari tabel kebenaran ini :

Penyelesaian :

a. Dalam bentuk SOP, maka yang dilihat adalah Y = 1

b. Dalam bentuk POS, maka yang dilihat adalah Y = 0